Prompted by a discussion on twitter, in which github.com/graphitemaster/normals_revisited was linked, I looked into this issue. It's pretty confusing!

Lets get into the details...

We can define the geometric normal of a triangle as the vector formed by taking the cross product of the triangle edges: $$n_g = (v_1 - v_0) \times (v_2 - v_0)$$ or $$n_g = a \times b$$ where \(a\) and \(b\) are the edge vectors $$a = v_1 - v_0$$ $$b = v_2 - v_0$$ This is assuming a counter-clockwise winding order convention.

The geometric normal transformed by some transformation \(M\) is given by the cross product of the transformed edges: $$n_g' = (Ma) \times (Mb)$$ From https://en.wikipedia.org/wiki/Cross_product, 'Algebraic properties', we have: $$n_g' = (Ma) \times (Mb) = det(M) (M^{-1})^T (a \times b)$$ Lets look in detail at the matrix $$det(M) (M^{-1})^T$$ To do this we introduce the adjugate matrix (https://en.wikipedia.org/wiki/Adjugate_matrix): $$adj(M) = cof(M)^T$$ Also from that wiki page, when the matrix M is invertible: $$adj(M) = det(M)M^{-1}$$ Therefore the matrix we had above is just the transpose of the adjugate: $$det(M) (M^{-1})^T = adj(M)^T$$ So the expression for the transformed normal becomes $$n_g' = det(M) (M^{-1})^T (a \times b)$$ $$n_g' = adj(M)^T (a \times b)$$ So, if we want to transform our normals like the geometric normal transforms, we definitely want to use the adjugate transpose, instead of the inverse transpose. BUT, do we want to transform our shading normals like the geometric normals? Generally we do, but lets look in detail at transformations with negative determinants. These are transformations with an odd number of reflections, such as a single reflection along the x-axis, e.g. in the y-z plane.

Consider R_x, which again is a reflection along the x-axis, e.g. in the y-z plane: $$ R_x = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$ It has the inverse $$ R_x^{-1} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = R_x $$ and also inverse transpose $$ {R_x^{-1}}^T = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}^T = R_x $$ The adjugate transpose however is different, as $$ det(R_x) = -1 $$ and so $$ adj(R_x) = det(R_x)R_x^{-1} = (-1)(R_x) $$ $$ adj(R_x) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} $$ and hence $$ adj(R_x)^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} $$ Now lets look graphically at how geometric normals transform under reflections. Consider the unit cube triangle mesh, and a couple of triangles on it, with geometric normals determined by counter-clockwise winding order and cross products:

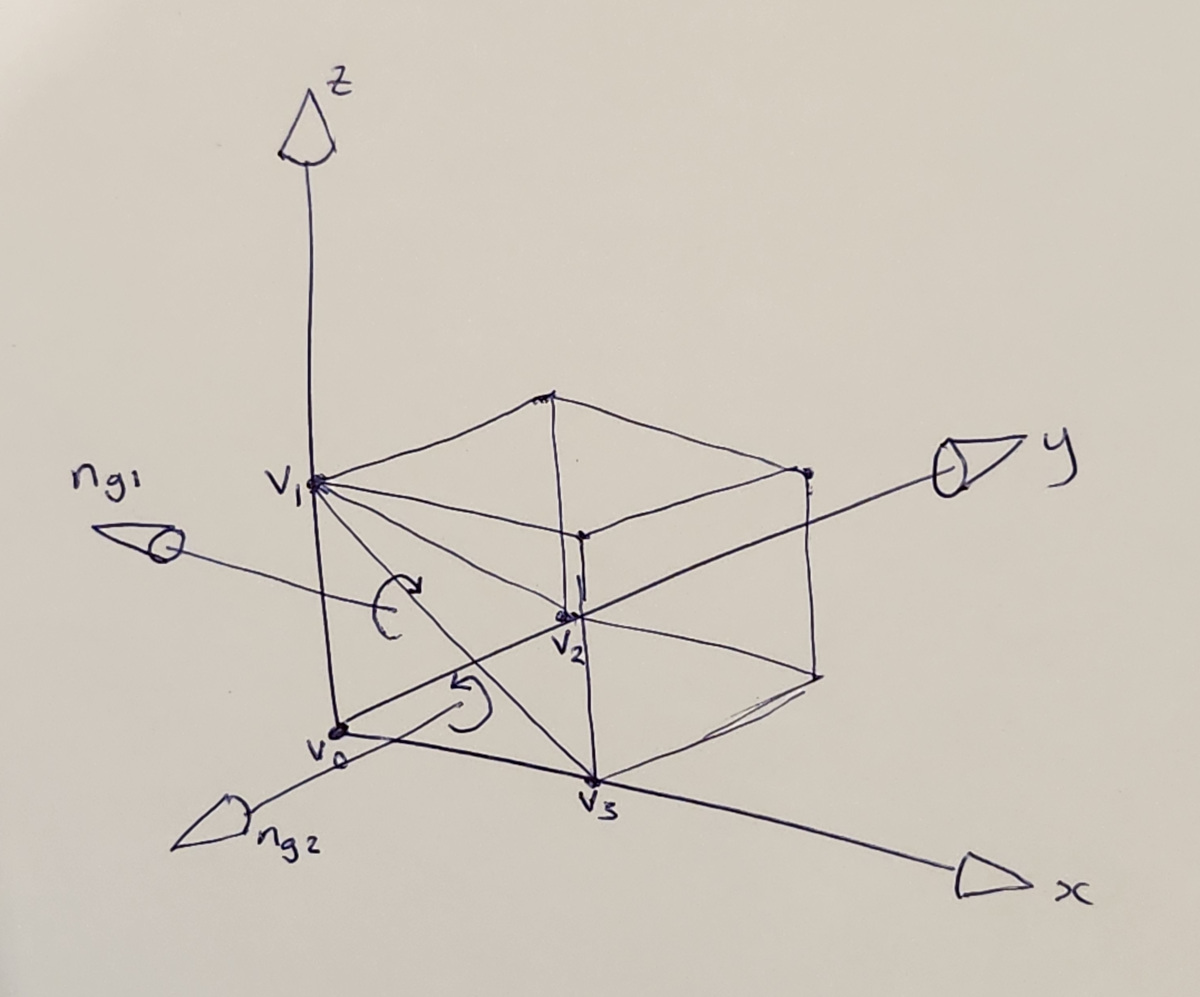The unit cube, with geometric normals

where the normals are given by the triangle edge cross products: $$ n_{g1} = (v_1 - v_0) \times (v_2 - v_0) = \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} $$ and $$ n_{g2} = (v_3 - v_0) \times (v_1 - v_0) = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} $$ Let's look what happens when we apply the transformation \(R_x\) to the cube vertices:

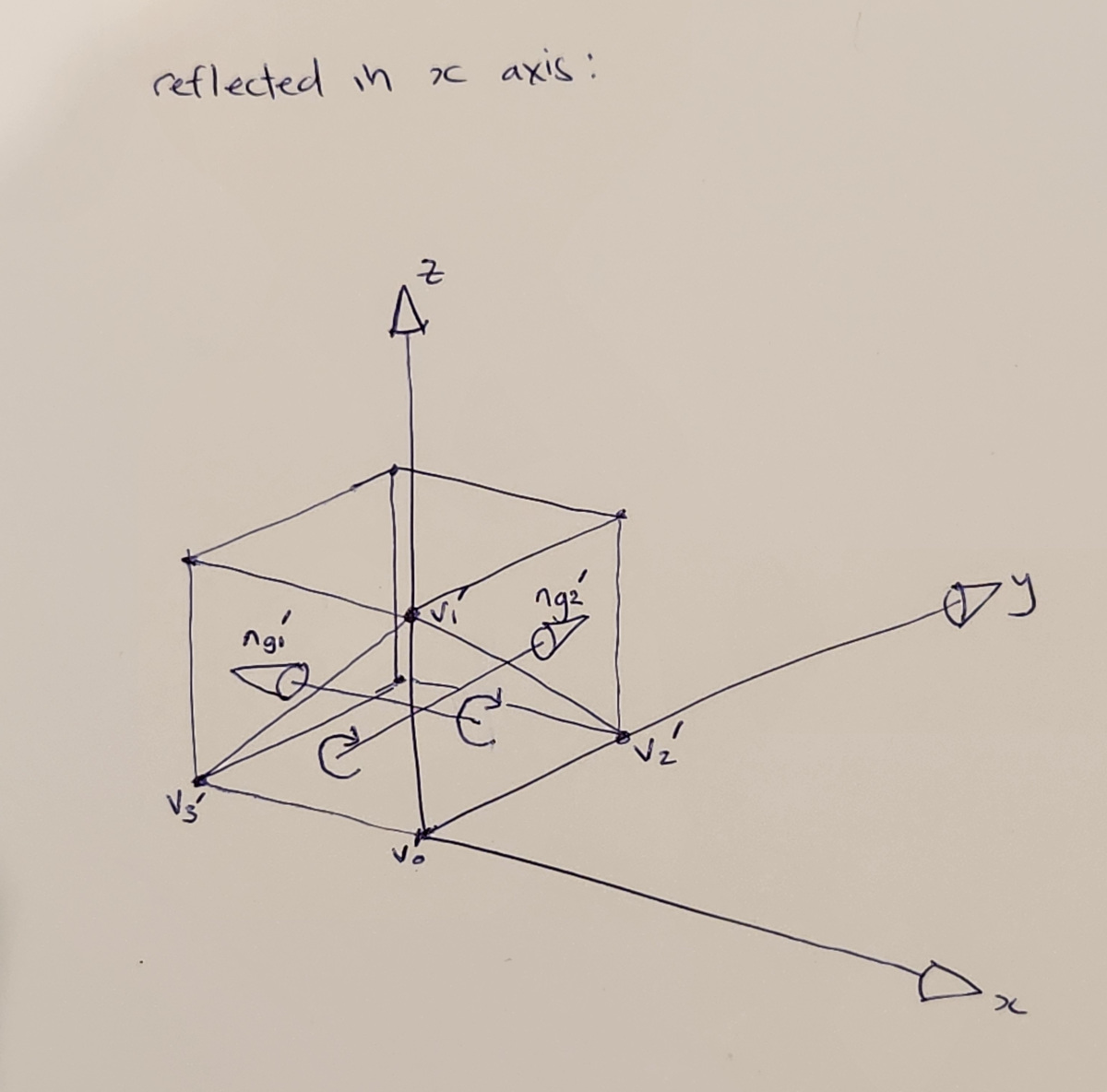The unit cube reflected along the x-axis, with resulting geometric normals

As you can see, reflecting the vertices in the x-axis (e.g. transforming by \(R_x\) results in the geometric normals pointing into the cube.

Let's see what the adjugate transpose and inverse transpose do to our normals:

First, let's try the adjugate tranpose: $$ n_{g1}' = adj(R_x)^T n_{g1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} $$ and $$ n_{g2}' = adj(R_x)^T n_{g2} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$ So it has flipped the y-direction normal, and as expected we get the normals that point into the transformed cube, as drawn.

Now lets try the inverse transpose: $$ n_{g1}' = {R_x^{-1}}^T n_{g1} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $$ and $$ n_{g2}' = {R_x^{-1}}^T n_{g2} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} $$ So it has instead flipped the x direction normal, and we end up with both normals pointing out of the transformed cube.

Note that this is probably what you want: generally you want normals to face out of objects.

So to repeat - under a transformation with a negative determinant, geometric normals that were pointing outwards will point inwards, and vice-versa. Since the adjugate transpose reproduces this behaviour, using it will result in normals pointing inwards that were pointing outwards. However the inverse transpose, due to having the extra determinant factor relative to the adjugate transpose, will flip/negate the normals so that they still point outwards.

So which should you use?

If you are never going to have transformations with negative determinants, or you are always going to flip your normals into the visible hemisphere, you can use the adjugate transpose. However if you do want to handle transformations with negative determinants, and you don't always flip your normals into the visible hemisphere, you might want to use the inverse transpose, or something like $$ sign(det(M)) adj(M)^T $$ which avoids a division.

Here are some result images from Substrata which demonstrate that the adjugate transpose doesn't handle reflection transforms well:

When there is no reflection transformation (just rotation and translation), both the adjugate transpose and sign(det) x adjugate transpose both give correct results:

Adjugate transpose used, no reflection transformation

sign(det) x Adjugate transpose used (similar to inverse transpose), no reflection transformation

However when there is a reflection transform, the adjugate transpose will make normals point into the mesh, which is probably not what you want, and gives incorrect lighting in my fragment shader:

Adjugate transpose used, with reflection transformation - incorrect rendering

However using \(sign(det(M)) adj(M)^T\) gives the correct result, as transformed normals are pointing outside the mesh:

sign(det) x Adjugate transpose used (similar to inverse transpose), with reflection transformation - correct rendering

Another very related issue I have come across, is that when doing back/front-face culling, you need to swap which faces you cull when the determinant is negative. E.g. if you usually cull backfaces, you want to cull frontfaces when the object determinant is negative. So you will need to compute the determinant anyway.

So which should you use? As mentioned earlier, it depends if your renderer needs to handle transformations with negative determinants (e.g. reflections) and if you flip your shading normals in your fragment shader anyway. I don't think there is a simple right and wrong choice.